
Prediction, Interpolation, Extrapolation. Prediction (interpolation ) and outlier detection: See sections 10.0.6.2. CaseĮstimated Response values (fitted values), residualsĪnd standardised residuals are presented in a table alongside observed Obtained from a multivariate regression run, after transforming the data intoĭisplayed in Common Regression table. Regression table and used in drawing the best fit lines in Plot. This information is displayed in the Separate The estimated parameters of the line of best fit for each This menu item is identical to the same one available under Parallel Line Method.

Response values for the i th preparation (i = Blank, Standard, Testġ, …, Test n – 1) and the j th dose level of the k th Predictions (interpolations) can be made for response orĭose values using the estimated model parameters. Multiple Assays with Combination and 10.0.2. If allĭose/treatment groups (or cells) have an equal number of replicates, or if theĭesign is balanced, then the plate effect is equivalent to Randomised Block Design.įor the other two optional variables and, see Variable is usually used to isolate a plate effect (or replicates). It isĬompulsory to select at least three columns, and Will be considered as the standard (with the exception of blanks). Otherwise the first preparation encountered in the column Preparation, but the first five characters of the standard preparation label shouldīe “stand” or “refer” in any language (capitalisation is not significant). the number of replicates forĮach dose-preparation combination may be different, dose levels for standardĪnd test preparations may be different, there can be more than one test An optional plate factor can be entered to keep track of plates or replicates.ĭesigns can be unbalanced, i.e. Second column contains the dose level for each measurement and anotherĬategorical column indicates which preparation a particular measurement belongs Measurement data is stacked in a single column, a The data format is as in Parallel Line Method (see 10.0.1.
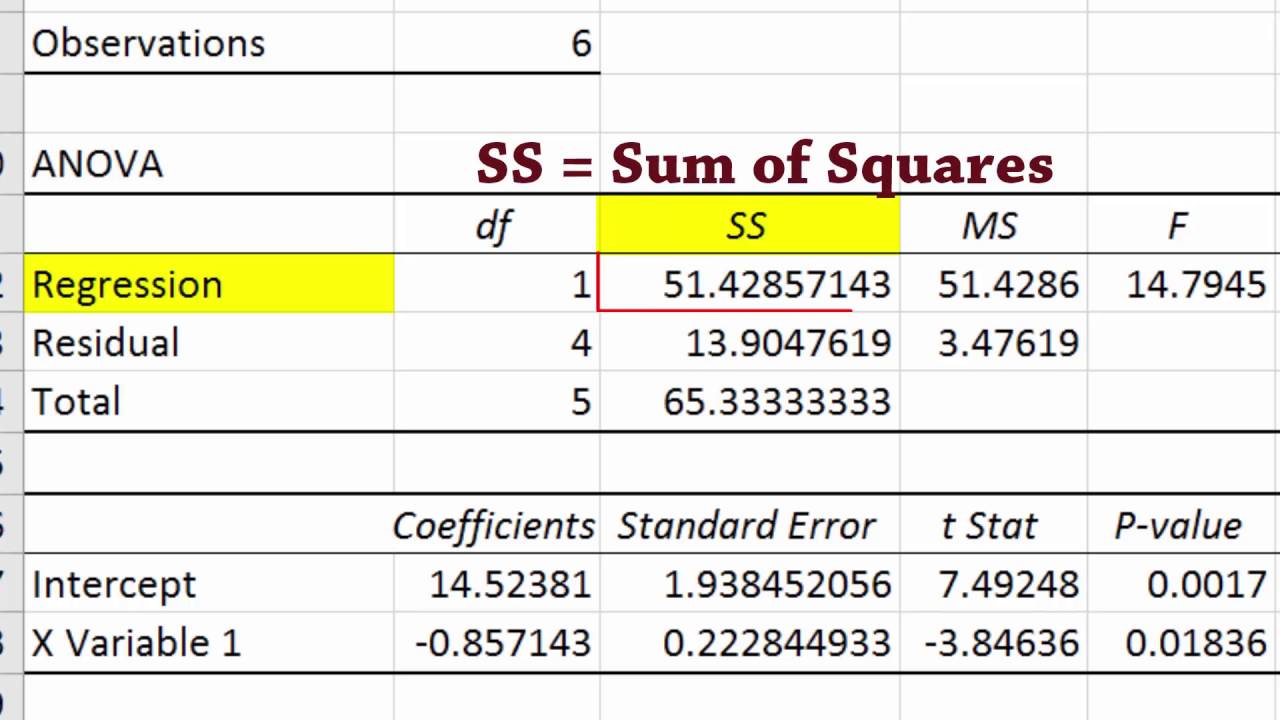
The Slope Ratio Method specification given in European Pharmacopoeia (1997-2017) is a restricted special case of this procedure. (row) effects and unlimited numbers of dose levels and test preparations. In fact changing 10 to any other value will produce another set of data with the same regression results.This is a general purpose procedure that can be used toĪnalyse balanced or unbalanced assays with blanks (0-dose treatments), plate Notice the regression coefficients are the same as the original data. Now create a new data set from the original data and compute the regression: x2 <- z$x + 10


The statistics you provide allow the construction of the linear regression line, but the confidence and prediction bands are narrowest at mean(x), mean(y) so without those you cannot compute them.Ī simple example may make this clearer. Without the original data you need one more piece of information: the means of the two variables. If the regression equation is reported as y = (-1.28106 +- 1.94918) + (1.00484 +- 0.03351) * x, R2 = 0.9017, p < 0.05, but the original data are not provided, how can I reproduce (at least approximately) the values, of the confidence and prediction intervals? Xy.pred <- predict.lm(xy.model, se.fit = TRUE, interval = "prediction", newdata = x.new)įor example, the confidence and prediction intervals of the first point are: xy.conf$fit Xy.conf <- predict.lm(xy.model, se.fit = TRUE, interval = "confidence", newdata = x.new) I calculate the confidence and prediction intervals: x.new <- ame(x = 1:npoints) # Residual standard error: 9.673 on 98 degrees of freedom This is a dummy dataset, with a line of slope 1 and gaussian noise 10: set.seed(1961) How could I calculate with this information the confidence and prediction intervals, or have a “reasonable” estimation? u(a1) and u(a2) are the uncertainties (standard error) of a1 and a2. In many fields of the natural sciences it is common practice to report the results of linear regression analysis as y = (a1 +- u(a1)) + (a2 +- u(a2)) * x, including R2 and p, but not the original data.


 0 kommentar(er)
0 kommentar(er)
